Difference between revisions of "Orange: Manifold Learning"
Onnowpurbo (talk | contribs) (Created page with "Sumber: https://docs.biolab.si//3/visual-programming/widgets/unsupervised/manifoldlearning.html Nonlinear dimensionality reduction. Inputs Data: input dataset Output...") |
Onnowpurbo (talk | contribs) |
||
| Line 15: | Line 15: | ||
Manifold Learning is a technique which finds a non-linear manifold within the higher-dimensional space. The widget then outputs new coordinates which correspond to a two-dimensional space. Such data can be later visualized with Scatter Plot or other visualization widgets. | Manifold Learning is a technique which finds a non-linear manifold within the higher-dimensional space. The widget then outputs new coordinates which correspond to a two-dimensional space. Such data can be later visualized with Scatter Plot or other visualization widgets. | ||
| − | + | [[File:Manifold-learning-stamped.png|center|200px|thumb]] | |
| + | |||
Method for manifold learning: | Method for manifold learning: | ||
| − | |||
t-SNE | t-SNE | ||
| − | |||
MDS, see also MDS widget | MDS, see also MDS widget | ||
| − | |||
Isomap | Isomap | ||
| − | |||
Locally Linear Embedding | Locally Linear Embedding | ||
| − | |||
Spectral Embedding | Spectral Embedding | ||
| − | |||
Set parameters for the method: | Set parameters for the method: | ||
| − | |||
t-SNE (distance measures): | t-SNE (distance measures): | ||
| − | |||
Euclidean distance | Euclidean distance | ||
| − | |||
Manhattan | Manhattan | ||
| − | |||
Chebyshev | Chebyshev | ||
| − | |||
Jaccard | Jaccard | ||
| − | |||
Mahalanobis | Mahalanobis | ||
| − | |||
Cosine | Cosine | ||
| − | |||
MDS (iterations and initialization): | MDS (iterations and initialization): | ||
| − | |||
max iterations: maximum number of optimization interactions | max iterations: maximum number of optimization interactions | ||
| − | |||
initialization: method for initialization of the algorithm (PCA or random) | initialization: method for initialization of the algorithm (PCA or random) | ||
| − | |||
Isomap: | Isomap: | ||
| − | |||
number of neighbors | number of neighbors | ||
| − | |||
Locally Linear Embedding: | Locally Linear Embedding: | ||
| − | |||
method: | method: | ||
| − | |||
standard | standard | ||
| − | |||
modified | modified | ||
| − | |||
hessian eigenmap | hessian eigenmap | ||
| − | |||
local | local | ||
| − | |||
number of neighbors | number of neighbors | ||
| − | |||
max iterations | max iterations | ||
| − | |||
Spectral Embedding: | Spectral Embedding: | ||
| − | |||
affinity: | affinity: | ||
| − | |||
nearest neighbors | nearest neighbors | ||
| − | |||
RFB kernel | RFB kernel | ||
| − | |||
Output: the number of reduced features (components). | Output: the number of reduced features (components). | ||
| − | |||
If Apply automatically is ticked, changes will be propagated automatically. Alternatively, click Apply. | If Apply automatically is ticked, changes will be propagated automatically. Alternatively, click Apply. | ||
| − | |||
Produce a report. | Produce a report. | ||
Manifold Learning widget produces different embeddings for high-dimensional data. | Manifold Learning widget produces different embeddings for high-dimensional data. | ||
| − | + | [[File:Collage-manifold.png|center|200px|thumb]] | |
From left to right, top to bottom: t-SNE, MDS, Isomap, Locally Linear Embedding and Spectral Embedding. | From left to right, top to bottom: t-SNE, MDS, Isomap, Locally Linear Embedding and Spectral Embedding. | ||
| − | + | ||
| + | ==Contoh== | ||
Manifold Learning widget transforms high-dimensional data into a lower dimensional approximation. This makes it great for visualizing datasets with many features. We used voting.tab to map 16-dimensional data onto a 2D graph. Then we used Scatter Plot to plot the embeddings. | Manifold Learning widget transforms high-dimensional data into a lower dimensional approximation. This makes it great for visualizing datasets with many features. We used voting.tab to map 16-dimensional data onto a 2D graph. Then we used Scatter Plot to plot the embeddings. | ||
| − | + | [[File:Manifold-learning-example.png|center|200px|thumb]] | |
| − | |||
Revision as of 09:22, 24 January 2020
Sumber: https://docs.biolab.si//3/visual-programming/widgets/unsupervised/manifoldlearning.html
Nonlinear dimensionality reduction.
Inputs
Data: input dataset
Outputs
Transformed Data: dataset with reduced coordinates
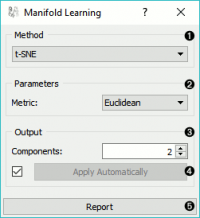
Manifold Learning is a technique which finds a non-linear manifold within the higher-dimensional space. The widget then outputs new coordinates which correspond to a two-dimensional space. Such data can be later visualized with Scatter Plot or other visualization widgets.
Method for manifold learning:
t-SNE
MDS, see also MDS widget
Isomap
Locally Linear Embedding
Spectral Embedding
Set parameters for the method:
t-SNE (distance measures):
Euclidean distance
Manhattan
Chebyshev
Jaccard
Mahalanobis
Cosine
MDS (iterations and initialization):
max iterations: maximum number of optimization interactions
initialization: method for initialization of the algorithm (PCA or random)
Isomap:
number of neighbors
Locally Linear Embedding:
method:
standard
modified
hessian eigenmap
local
number of neighbors
max iterations
Spectral Embedding:
affinity:
nearest neighbors
RFB kernel
Output: the number of reduced features (components).
If Apply automatically is ticked, changes will be propagated automatically. Alternatively, click Apply.
Produce a report.
Manifold Learning widget produces different embeddings for high-dimensional data.
From left to right, top to bottom: t-SNE, MDS, Isomap, Locally Linear Embedding and Spectral Embedding.
Contoh
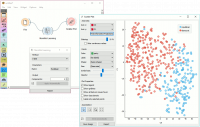
Manifold Learning widget transforms high-dimensional data into a lower dimensional approximation. This makes it great for visualizing datasets with many features. We used voting.tab to map 16-dimensional data onto a 2D graph. Then we used Scatter Plot to plot the embeddings.